irl-patrolling

Learning Patrolling Path via Inverse Reinforcement Learning

Project consists of a MATLAB component for Inverse Reinforcement Learning of patrolling paths generated using the Open Motion Planning Library, and a Python script to visualize the polcies as a new trajectory.

Introduction

Patrolling is the problem of repeatedly visiting a group of regions in an environment. This problem has applications in different areas such as environmental monitoring, infrastructure surveillance, and border security. This problem is also important because in its multi-agent version, the action of patrolling is carried by multiple robots as patrollers working together to ensure adversarial intrusion or co-operate other robots. This is also useful for computational models of animal and human learning.

Motivation

Motivation

How can we recover an expert's underlying reward function more easily than having to learn the expert's policy? After all, an expert may only have a rough idea of the reward function that generates desirable behavior. It's also interesting to recover experts underlying reward function, which can be done more cheaply than learning expert's policy.When learning a new patrolling trajectory, it's easy to follow the expert's paths instead of specifying a reward function for those paths. This learning from an expert's demonstration is called apprenticeship learning, or learning from demonstration. It is when instead of giving a reward function, we instead give some expert policies, value function, and transition probabilities. Then the reward function is learned.

Some existing applications for IRL include things such as autonomous driving and parking, and modeling human and animal behaviors. This problem can be extended to many patrolling situations, such as guarding a museum.

Problem Formulation

• State space
• Action space
• Transition probabilities
• Discount factor
• Expert demonstrations

Via Inverse Reinforcement Learning, can we recover a reward function R? Moreover, can we use this R to find a good policy?

Method

Data

The expert trajectories were generated in the Open Motion Planning Library (OMPL). OMPL is a set of sampling-based motion planning algorithms. Here, we give an environment and a series of way-points that we want to cover. Next, a semi-random path is generated using Rapidly-Exploring Random Trees (RRT-Connect). We input the requirements into a planner and then run the simulation, changing the settings until we achieved a somewhat realistic portrayal of what a guard might do when patrolling. Next, the trajectories were taken and then modified to be the input for the IRL algorithm. This yields a feature vector over states.

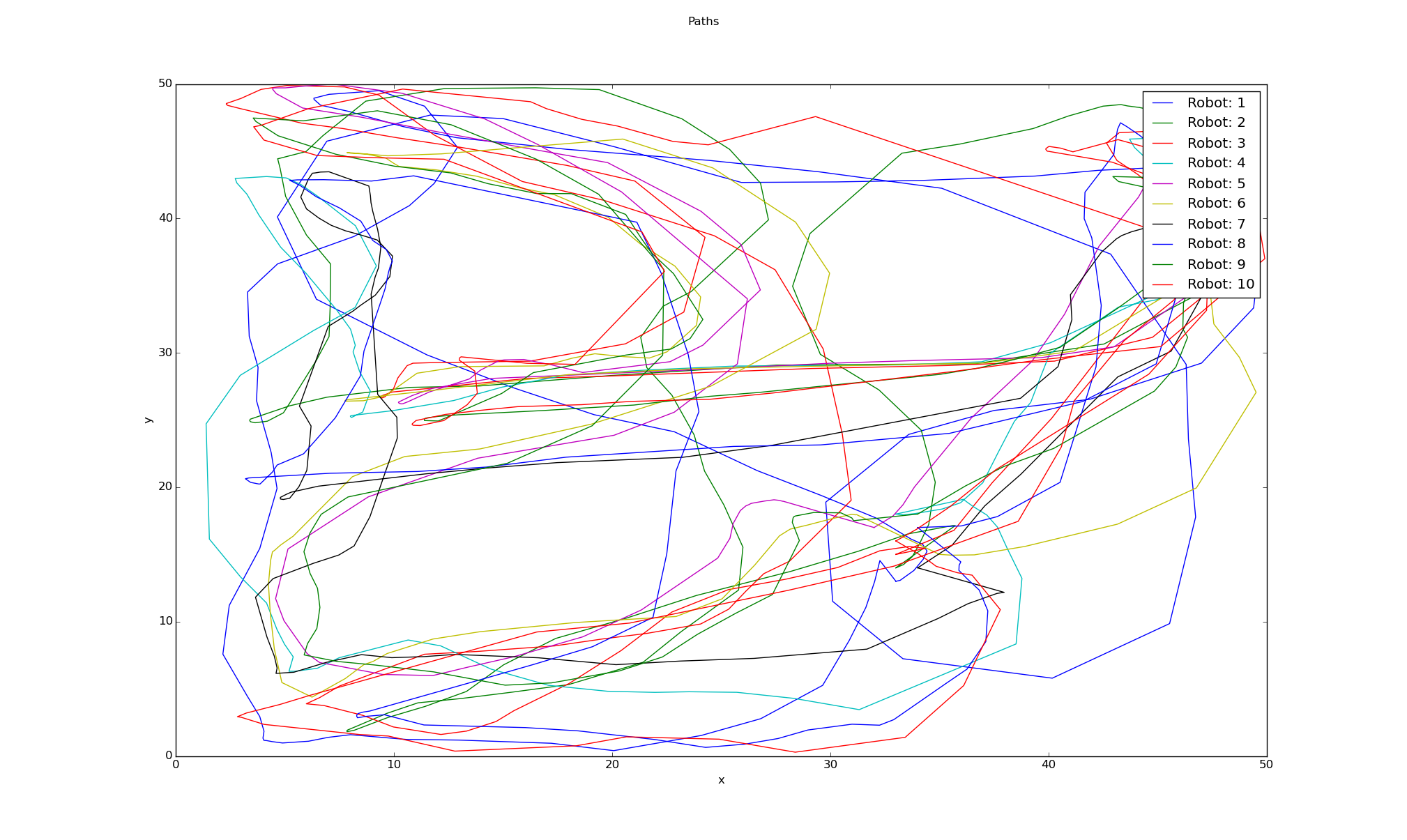
Computation

We begin with an environment that consists of a grid of cells. Each cell represents an area of the discretized environment. We have a reward function that we want to maximize; and policies where each policy has a corresponding feature expectation vector.

First randomly pick an expert policy. Then iterate, and guess the reward function, such that the expert maximally outperforms the policies that were previously generated. This was then broken up into macrocells in order to simplify both computation and the output.

In the suboptimal case, the policy is a mix of arbitrary policies, which have an expert in their convex hull. In practice, we pick the best one from the set along with the corresponding reward function.

We input the trajectories into the matlab simulation in order to generate a reward function. Then, the learned trajectory was calculated by taking the average reward value of each macrocell. This simulation will then yield a final, complete trajectory that closely approximates the given way-points. This was then done multiple times in order to generate the set of "expert patrolling paths" that were used as input for the rest of the project. Finally, this was then converted into an average which was used to generate the final trajectory.

Results

In the end, we have used the reward values to learn a new patrolling path for robot to follow via a greedy approach. The newly learned patrolling path is better than the expert's patrolling paths or close to the expert's patrolling paths. The strength of our work is that the learning of patrolling path has been automated and it's reasonably good patrolling considering the zig-zag patrolling paths given by expert.

These results are especially useful for patrolling situations where we can benefit from previously learned trajectories. For example, a museum may analyze their night-guard paths and use them to generate an optimal policy so that a robot can assist in the rounds.

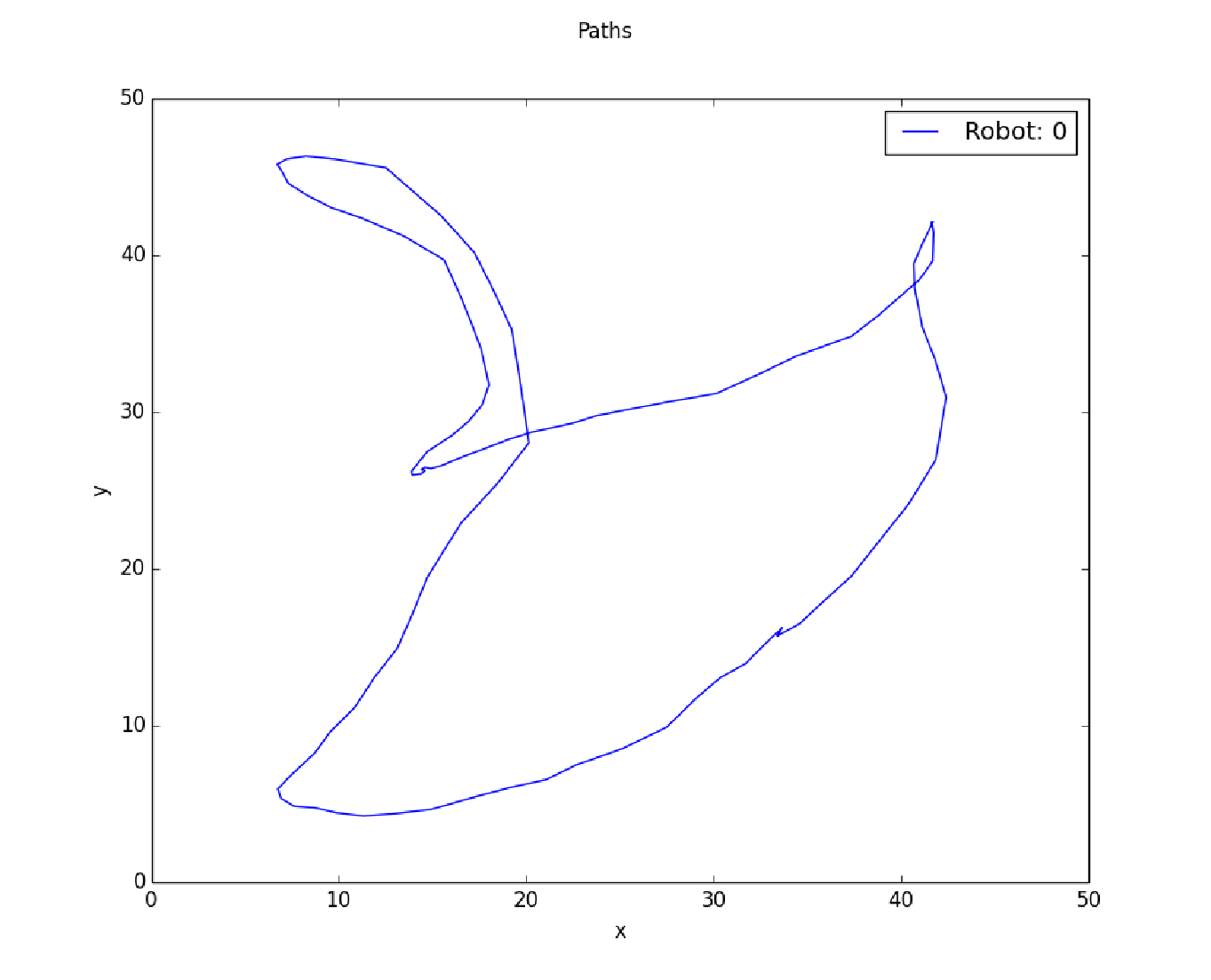
Future Work

• In our work, we haven't used obstacles inside the environment which is more pragmatic scenario. In that scenario, we will have to incorporate obstacle avoidance techniques for newly learned patrolling path. This way, we can have things like walls, buildings, or perhaps even moving obstacles so that the reward function will also take these into account and avoid them.
• Another issue that we hope to address in the future is that we have used the greedy approach to apply reward values to generate new learned patrolling paths. A more optimized approach for example maximizing the reward values can lead the learned patrolling path towards a optimal patrolling path. For example, we could use Dijkstra or A* search in order to yield a more optimal path through the grid.

References

• P. Abbeel and A. Y. Ng. Apprenticeship learning via inverse reinforcement learning. In proceedings of ICML, pages 1–8, 2004.
• J. A. B. B. D. Ziebart, A. Maas and A. K. Dey. Maximum entropy inverse reinforcement learning. In proceedings of AAAI, pages 1433–1439, 2008.
• [3] A. T. K. Mombaur and J.-P. Laumond. From human to humanoid locomotionan inverse optimal control approach. In Autonomous Robots (AURO), 28:369–383, 2010.
• S. Levine. Nonlinear inverse reinforcement learning with gaussian processes, 2011.
• A. Y. Ng and S. Russell. Algorithms for inverse reinforcement learning. In proceedings of ICML, pages 663–670, 2000.
• A. Y. N. P. Abbeel, D. Dolgov and S. Thrun. Apprenticeship learning for motion planning with application to parking lot navigation. In proceedings of international conference on intelligent robots and systems (IROS), pages 1083–1090, 2008.
• B. Ratliff and Zinkevich. Aerial imagery based navigation. In proceedings of ICML, 2006.
• I. A. S ̧ucan, M. Moll, and L. E. Kavraki. The Open Motion Planning Library. IEEE Robotics & Automation Magazine, 19(4):72–82, December 2012. http://ompl.kavrakilab.org.